Produit vectoriel : Cours – Résumés – Exercices TD TP EXAMENS

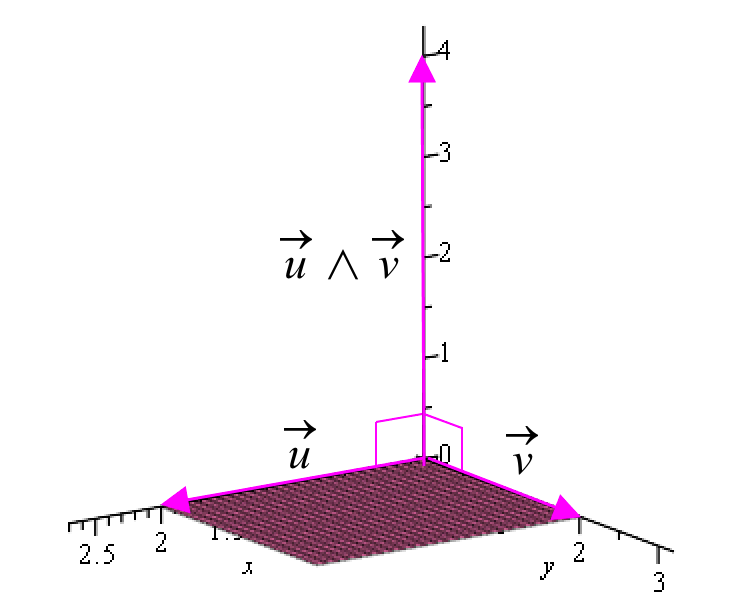
Le produit vectoriel de deux vecteurs \vec { u } et\vec { v } est le vecteur \vec { w } =\vec { u } \wedge \vec { v } définit par :

Sa direction est perpendiculaire au plan (\vec { u } ,\vec { v } )
Son sens est tel que le trièdre (\vec { u } ,\vec { v } ,\vec { w } ) est direct
Sa norme est : \left| \vec { u } \right| .\left| \vec { v } \right| .\left| \sin { (\vec { u } ,\vec { v } } \right|

Propriétés

\vec { u } \wedge \vec { v } =-(\vec { v } \wedge \vec { u } )
\vec { u } \wedge (\vec { v } +\vec { w } )=\vec { u } \wedge \vec { v } +\vec { u } \wedge \vec { w }
(\vec { u } +\vec { v } )\wedge \vec { w } =\vec { u } \wedge \vec { w } +\vec { v } \wedge \vec { w }
(k\vec { u } )\wedge \vec { v } =\vec { u } \wedge (k\vec { v } )=k(\vec { u } \wedge \vec { v } )
Si \vec { u } et\vec { v } sont colinéaires \vec { u } \wedge \vec { v } =\vec { 0 }

Produit vectoriel dans une base orthonormée

Si $(\vec { i } ,\vec { j } ,\vec { k } )$ est une base orthonormée de plan, on vérifie facilement que :

\vec { i } \wedge \vec { j } =\vec { k }
\vec { j } \wedge \vec { k } =\vec { i }
\vec { k } \wedge \vec { i } =\vec { j }
\vec { j } \wedge \vec { i } =-\vec { k }
\vec { k } \wedge \vec { j } =-\vec { i }
\vec { i } \wedge \vec { k } =-\vec { j }
\vec { i } \wedge \vec { i } =\vec { j } \wedge \vec { j } =\vec { k } \wedge \vec { k } =0

Applications du produit vectoriel

a-Calcul d’aire d’un triangle/parallélogramme

L’aire A d’un triangle ABC est donnée par :

S=\frac { 1 }{ 2 } \left| \vec { AB } \wedge \vec { AC } \right|

Démonstration : Soit ABC un triangle. On considère la hauteur issue de C. On note h sa longueur.

S=\frac { AB\times h }{ 2 } =\frac { AB\times AC\sin { \alpha } }{ 2 } =\frac { 1 }{ 2 } \left| \vec { AB } \wedge \vec { AC } \right|

clubsuit L’aire d’un parallélogramme étant le double de l’aire du triangle formé par trois sommets de ce parallélogramme, on a:

S=\left| \vec { AB } \wedge \vec { AC } \right|

b- Moment d’une force

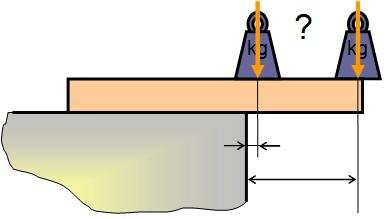
Moment d’une force - application du produit vectoriel

Soit une planche en équilibre au bord d’un muret. Pour la déséquilibrer, on peut poser une charge sur la partie en porte-à-faux, au-dessus du vide. La capacité de cette charge à faire basculer la planche n’est pas la même suivant qu’elle est posée près du muret ou au bout de la planche. De même on peut, au même endroit, placer une charge plus lourde et constater une différence de basculement.

Le « pouvoir de basculement »dépend donc de l’intensité de la force, mais également de la position relative du point d’application de la force, et du point de rotation réel ou virtuel considéré.

On intègre ces trois composantes du problème par le modèle de moment d’une force, qui représente l’aptitude d’une force à faire tourner un système mécanique autour d’un point donné, qu’on nommera pivot.

Le moment d’une force F s’exerçant au point P par rapport au pivot O, est le vecteur:

\vec { M } =\vec { OP } \wedge \vec { F }

où ∧ désigne le produit vectoriel.

Pour plus de détails télécharger les documents ci-dessous:

Liens de téléchargement des cours sur le Produit vectoriel

Cours sur le Produit vectoriel N°1